Car旅行
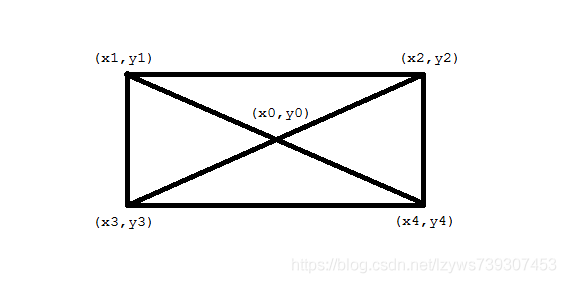
已知矩形三个顶点求第四个
-
确定直角点:可以判断(x2-x1)*(x3-x1)+(y2-y1)*(y3-y1)是否为0,如果为0,则证明点(x1,y1)即为直角点,如果不是,我们继续判断(x2,y2),(x3,y3),这三个点肯定有一个是直角点。
-
利用对角线上的点横坐标之和等于中点横坐标的二倍这个方法求出
-
若已知直角点为x3,y3,那么通过x1,y1和x4,y4可以得到x0,y0,从而延长一倍得到x2,y2
存图
每个机场之间都有航线,这使得用邻接表存图没有意义,因为这个题相当于是个完全图,因此使用邻接矩阵存图
最短路径算法解决
基本最短路算法,但是是多源的。不能只使用一个dijkstra
-
floyd
-
4次Dijkstra

注意:double的极大值可以赋值为1e100
神经网络
这一题就是激活输入层,看看输出层的值是多少。
拓扑排序的变式就可以【+模拟】,一层层传达到输出
- 确定输出层和输入层?
- 给出了边的信息,只要记录出度就知道了,出度为0的肯定是输出层。
- 记录入度就能确定哪个是输入层
- 阈值怎么处理?
- 直接在输入时提前减去就好【c[i]=c[i]-u[i]】,接着只要判断c[i]经过边更新是否大于0就好了。
- 本题坑点:第一层不适用公式,保证会激活,不在意阈值
为什么要用拓扑排序
简单一句话:【从公式知】所有的节点的权值是从他的上一个节点推过来的,所以这是DAG上的递推关系,我们一般用拓扑排序做。 \(先看题目公式:C[i]=\sum\limits_{(j,i)\in E}{W_{(j,i)}}*C[j]-U[i]\)
\[发现要想求出 C[i] 就要求出所有C[j] (i,j\in E)的值。\]- 举个栗子:
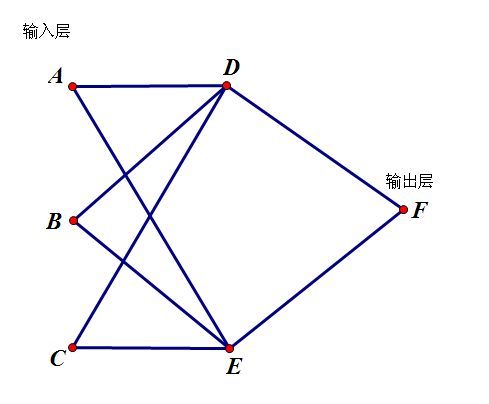
- 对于上面这个图,想要算出 F的 C值,就要先算出D和 E的 C 值,也就是要算所有入边的情况【得到某一个点的值必须要计算所有入边的值——拓扑排序】
- 这不就是赤裸裸的拓扑排序吗?
- 从上面那个图还可以看出,输入层是入度为0的点(A、B、C),输出层是出度为 0 的点(F),如果你用的是邻接表存图你可以只记录入度不记录出度,因为一个点 u出度为 0相当于 head[u]==0,所以输出的时候判断每个点的 head和 C就好了。
注意:本题没有说正整数,因此要格外小心,阈值和边权都可能为负数
最长递增子序列DP算法优化后O(nlogn)
问题描述
给出长度为N的数组,找出这个数组的最长递增子序列。(递增子序列是指,子序列的元素是递增的) 例如:5 1 6 8 2 4 5 10,最长递增子序列是1 2 4 5 10。
最长递增子序列,即Longest Increasing Subsequence 常常被简记为 LIS。 常见的n²算法:
- 排序+LCS算法:转换为最长公共子序列[LCS]问题。如例子中的数组A{5,6, 7, 1, 2, 8},则我们排序该数组得到数组A‘{1, 2, 5, 6, 7, 8},然后找出数组A和A’的最长公共子序列即可。
- DP算法:设长度为N的数组为{a0,a1, a2, …an-1),则假定以aj结尾的数组序列的最长递增子序列长度为L(j),则L(j)={ max(L(i))+1, i<j且a[i]<a[j] }。也就是说,我们需要遍历在j之前的所有位置i(从0到j-1),找出满足条件a[i]<a[j]的L(i),求出max(L(i))+1即为L(j)的值。最后,我们遍历所有的L(j)(从0到N-1),找出最大值即为最大递增子序列。
由于较为常见这里就忽略了。详细可见最长递增子序列算法
优化后的O(nlogn)算法
假设存在一个序列d[1..9] = {2 1 5 3 6 4 8 9 7},可以看出来它的LIS长度为5。
下面一步一步试着找出它。
定义一个序列B,然后令 i = 1 to 9 逐个考察这个序列。 具体的算法思想:建立一个空序列M,把d序列中的元素从下标1到9逐一有序地插入新序列M。判断新增这个元素后,长度为i【例子中为:1到9】时,有序序列M中的最小末尾元素【假设为K】,更新相应的B[i]=K。 此外,我们用一个变量Len来记录现在最长算到多少了
首先,把d[1]有序地放到B里,令B[1] = 2,就是说当只有1一个数字2的时候,长度为1的LIS的最小末尾是2。这时Len=1
然后,把d[2]有序地放到B里,令B[1] = 1,就是说长度为1的LIS的最小末尾是1,d[1]=2已经没用了,很容易理解吧。这时Len=1
接着,d[3] = 5,d[3]>B[1],所以令B[1+1]=B[2]=d[3]=5,就是说长度为2的LIS的最小末尾是5,很容易理解吧。这时候B[1..2] = 1, 5,Len=2
再来,d[4] = 3,它正好加在1,5之间,放在1的位置显然不合适,因为1小于3,长度为1的LIS最小末尾应该是1,这样很容易推知,长度为2的LIS最小末尾是3,于是可以把5淘汰掉,这时候B[1..2] = 1, 3,Len = 2
继续,d[5] = 6,它在3后面,因为B[2] = 3, 而6在3后面,于是很容易可以推知B[3] = 6, 这时B[1..3] = 1, 3, 6,还是很容易理解吧? Len = 3 了噢。
第6个, d[6] = 4,你看它在3和6之间,于是我们就可以把6替换掉,得到B[3] = 4。B[1..3] = 1, 3, 4, Len继续等于3
第7个, d[7] = 8,它很大,比4大,嗯。于是B[4] = 8。Len变成4了
第8个, d[8] = 9,得到B[5] = 9,嗯。Len继续增大,到5了。
最后一个, d[9] = 7,它在B[3] = 4和B[4] = 8之间,所以我们知道,最新的B[4] =7,B[1..5] = 1, 3, 4, 7, 9,Len = 5。
于是我们知道了LIS的长度为5。
!!!!! 注意。这个1,3,4,7,9不是LIS,它只是存储的对应长度LIS的最小末尾。有了这个末尾,我们就可以一个一个地插入数据。虽然最后一个d[9] = 7更新进去对于这组数据没有什么意义,但是如果后面再出现两个数字 8 和 9,那么就可以把8更新到d[5], 9更新到d[6],得出LIS的长度为6。
然后应该发现一件事情了:在B中插入数据是有序的,而且是进行替换而不需要挪动——也就是说,我们可以使用二分查找,将每一个数字的插入时间优化到O(logN)~~~~~于是算法的时间复杂度就降低到了O(NlogN)~!